We Do It Again and Get a 5 and the Array 2 1 0 0 0 0 0 0
NumPy quickstart¶
Prerequisites¶
You'll need to know a chip of Python. For a refresher, see the Python tutorial.
To work the examples, you'll need matplotlib installed in addition to NumPy.
Learner profile
This is a quick overview of arrays in NumPy. Information technology demonstrates how n-dimensional (\(north>=ii\)) arrays are represented and tin be manipulated. In particular, if you don't know how to use mutual functions to n-dimensional arrays (without using for-loops), or if you want to understand centrality and shape properties for n-dimensional arrays, this article might be of help.
Learning Objectives
Afterward reading, you should be able to:
-
Empathize the difference between 1-, two- and n-dimensional arrays in NumPy;
-
Understand how to apply some linear algebra operations to n-dimensional arrays without using for-loops;
-
Understand axis and shape properties for n-dimensional arrays.
The Basics¶
NumPy'due south principal object is the homogeneous multidimensional assortment. Information technology is a table of elements (usually numbers), all of the aforementioned type, indexed by a tuple of non-negative integers. In NumPy dimensions are called axes.
For instance, the array for the coordinates of a point in 3D space, [1, ii, 1] , has 1 axis. That axis has 3 elements in it, and then we say it has a length of 3. In the example pictured below, the array has two axes. The offset axis has a length of ii, the second axis has a length of 3.
[[ ane. , 0. , 0. ], [ 0. , 1. , 2. ]] NumPy's array course is called ndarray . It is likewise known by the allonym array . Note that numpy.array is not the same as the Standard Python Library class array.assortment , which but handles one-dimensional arrays and offers less functionality. The more important attributes of an ndarray object are:
- ndarray.ndim
-
the number of axes (dimensions) of the array.
- ndarray.shape
-
the dimensions of the array. This is a tuple of integers indicating the size of the array in each dimension. For a matrix with n rows and chiliad columns,
shapevolition be(n,m). The length of theshapetuple is therefore the number of axes,ndim. - ndarray.size
-
the total number of elements of the array. This is equal to the product of the elements of
shape. - ndarray.dtype
-
an object describing the blazon of the elements in the array. One can create or specify dtype'south using standard Python types. Additionally NumPy provides types of its own. numpy.int32, numpy.int16, and numpy.float64 are some examples.
- ndarray.itemsize
-
the size in bytes of each element of the array. For example, an array of elements of type
float64hasitemsize8 (=64/8), while i of typecomplex32hasitemsize4 (=32/viii). It is equivalent tondarray.dtype.itemsize. - ndarray.information
-
the buffer containing the actual elements of the array. Normally, we won't need to use this attribute because nosotros will access the elements in an array using indexing facilities.
An example¶
>>> import numpy every bit np >>> a = np . arange ( 15 ) . reshape ( 3 , 5 ) >>> a assortment([[ 0, 1, 2, 3, four], [ five, 6, 7, 8, ix], [x, 11, 12, 13, xiv]]) >>> a . shape (3, 5) >>> a . ndim two >>> a . dtype . proper name 'int64' >>> a . itemsize 8 >>> a . size 15 >>> type ( a ) <class 'numpy.ndarray'> >>> b = np . array ([ 6 , 7 , eight ]) >>> b array([six, 7, 8]) >>> type ( b ) <class 'numpy.ndarray'> Array Creation¶
At that place are several means to create arrays.
For instance, you tin create an array from a regular Python list or tuple using the assortment function. The type of the resulting array is deduced from the type of the elements in the sequences.
>>> import numpy as np >>> a = np . array ([ 2 , 3 , four ]) >>> a array([ii, 3, 4]) >>> a . dtype dtype('int64') >>> b = np . array ([ 1.2 , 3.five , 5.1 ]) >>> b . dtype dtype('float64') A frequent mistake consists in calling array with multiple arguments, rather than providing a single sequence as an argument.
>>> a = np . array ( 1 , 2 , 3 , four ) # Incorrect Traceback (most recent call last): ... TypeError: array() takes from 1 to 2 positional arguments but iv were given >>> a = np . array ([ 1 , 2 , iii , 4 ]) # RIGHT array transforms sequences of sequences into two-dimensional arrays, sequences of sequences of sequences into 3-dimensional arrays, and so on.
>>> b = np . assortment ([( 1.five , 2 , three ), ( 4 , 5 , half dozen )]) >>> b array([[ane.v, ii. , three. ], [4. , 5. , 6. ]]) The blazon of the assortment tin also be explicitly specified at creation time:
>>> c = np . array ([[ 1 , 2 ], [ 3 , 4 ]], dtype = complex ) >>> c array([[i.+0.j, ii.+0.j], [three.+0.j, 4.+0.j]]) Often, the elements of an array are originally unknown, merely its size is known. Hence, NumPy offers several functions to create arrays with initial placeholder content. These minimize the necessity of growing arrays, an expensive operation.
The function zeros creates an array full of zeros, the function ones creates an assortment full of ones, and the role empty creates an array whose initial content is random and depends on the country of the retentiveness. Past default, the dtype of the created array is float64 , but it can be specified via the key word statement dtype .
>>> np . zeros (( 3 , 4 )) array([[0., 0., 0., 0.], [0., 0., 0., 0.], [0., 0., 0., 0.]]) >>> np . ones (( ii , three , iv ), dtype = np . int16 ) array([[[1, 1, i, i], [1, 1, 1, 1], [ane, one, 1, 1]], [[1, 1, 1, ane], [i, ane, i, one], [1, 1, i, one]]], dtype=int16) >>> np . empty (( 2 , 3 )) array([[3.73603959e-262, six.02658058e-154, 6.55490914e-260], # may vary [5.30498948e-313, 3.14673309e-307, 1.00000000e+000]]) To create sequences of numbers, NumPy provides the arange office which is coordinating to the Python born range , but returns an array.
>>> np . arange ( ten , 30 , v ) array([10, 15, 20, 25]) >>> np . arange ( 0 , 2 , 0.three ) # it accepts bladder arguments array([0. , 0.3, 0.6, 0.9, i.2, ane.5, one.8]) When arange is used with floating point arguments, it is generally not possible to predict the number of elements obtained, due to the finite floating point precision. For this reason, it is commonly better to use the function linspace that receives as an argument the number of elements that we want, instead of the step:
>>> from numpy import pi >>> np . linspace ( 0 , 2 , ix ) # nine numbers from 0 to 2 array([0. , 0.25, 0.5 , 0.75, 1. , 1.25, 1.v , 1.75, ii. ]) >>> ten = np . linspace ( 0 , two * pi , 100 ) # useful to evaluate function at lots of points >>> f = np . sin ( x ) Encounter too
array , zeros , zeros_like , ones , ones_like , empty , empty_like , arange , linspace , numpy.random.Generator.rand, numpy.random.Generator.randn, fromfunction , fromfile
Printing Arrays¶
When you impress an array, NumPy displays it in a similar way to nested lists, merely with the following layout:
-
the last centrality is printed from left to right,
-
the second-to-last is printed from top to bottom,
-
the balance are also printed from top to bottom, with each slice separated from the adjacent by an empty line.
1-dimensional arrays are then printed equally rows, bidimensionals equally matrices and tridimensionals as lists of matrices.
>>> a = np . arange ( 6 ) # 1d array >>> print ( a ) [0 i 2 3 4 five] >>> >>> b = np . arange ( 12 ) . reshape ( 4 , 3 ) # 2nd array >>> impress ( b ) [[ 0 i 2] [ iii iv 5] [ 6 7 8] [ 9 ten xi]] >>> >>> c = np . arange ( 24 ) . reshape ( 2 , 3 , 4 ) # 3d array >>> print ( c ) [[[ 0 1 2 3] [ 4 v half-dozen 7] [ 8 9 10 11]] [[12 13 14 15] [xvi 17 eighteen 19] [twenty 21 22 23]]] Encounter below to get more details on reshape .
If an array is too large to be printed, NumPy automatically skips the cardinal part of the assortment and only prints the corners:
>>> impress ( np . arange ( 10000 )) [ 0 1 2 ... 9997 9998 9999] >>> >>> impress ( np . arange ( 10000 ) . reshape ( 100 , 100 )) [[ 0 ane 2 ... 97 98 99] [ 100 101 102 ... 197 198 199] [ 200 201 202 ... 297 298 299] ... [9700 9701 9702 ... 9797 9798 9799] [9800 9801 9802 ... 9897 9898 9899] [9900 9901 9902 ... 9997 9998 9999]] To disable this behaviour and strength NumPy to print the entire array, you can change the printing options using set_printoptions .
>>> np . set_printoptions ( threshold = sys . maxsize ) # sys module should be imported Basic Operations¶
Arithmetic operators on arrays apply elementwise. A new assortment is created and filled with the issue.
>>> a = np . array ([ 20 , thirty , 40 , 50 ]) >>> b = np . arange ( 4 ) >>> b array([0, 1, ii, iii]) >>> c = a - b >>> c array([20, 29, 38, 47]) >>> b ** ii array([0, 1, 4, 9]) >>> 10 * np . sin ( a ) array([ 9.12945251, -9.88031624, 7.4511316 , -two.62374854]) >>> a < 35 array([ True, True, Imitation, Simulated]) Unlike in many matrix languages, the product operator * operates elementwise in NumPy arrays. The matrix product can be performed using the @ operator (in python >=3.five) or the dot function or method:
>>> A = np . array ([[ 1 , i ], ... [ 0 , 1 ]]) >>> B = np . array ([[ 2 , 0 ], ... [ 3 , 4 ]]) >>> A * B # elementwise product array([[two, 0], [0, 4]]) >>> A @ B # matrix product assortment([[5, 4], [3, 4]]) >>> A . dot ( B ) # another matrix production array([[v, 4], [three, 4]]) Some operations, such equally += and *= , act in place to modify an existing array rather than create a new i.
>>> rg = np . random . default_rng ( ane ) # create example of default random number generator >>> a = np . ones (( 2 , 3 ), dtype = int ) >>> b = rg . random (( 2 , iii )) >>> a *= 3 >>> a array([[3, 3, 3], [3, 3, iii]]) >>> b += a >>> b array([[3.51182162, 3.9504637 , iii.14415961], [3.94864945, 3.31183145, 3.42332645]]) >>> a += b # b is non automatically converted to integer type Traceback (virtually recent call final): ... numpy.core._exceptions._UFuncOutputCastingError: Cannot cast ufunc 'add' output from dtype('float64') to dtype('int64') with casting rule 'same_kind' When operating with arrays of different types, the type of the resulting array corresponds to the more than general or precise one (a beliefs known as upcasting).
>>> a = np . ones ( three , dtype = np . int32 ) >>> b = np . linspace ( 0 , pi , 3 ) >>> b . dtype . name 'float64' >>> c = a + b >>> c array([1. , two.57079633, 4.14159265]) >>> c . dtype . name 'float64' >>> d = np . exp ( c * 1 j ) >>> d array([ 0.54030231+0.84147098j, -0.84147098+0.54030231j, -0.54030231-0.84147098j]) >>> d . dtype . name 'complex128' Many unary operations, such every bit calculating the sum of all the elements in the array, are implemented as methods of the ndarray class.
>>> a = rg . random (( ii , 3 )) >>> a array([[0.82770259, 0.40919914, 0.54959369], [0.02755911, 0.75351311, 0.53814331]]) >>> a . sum () 3.1057109529998157 >>> a . min () 0.027559113243068367 >>> a . max () 0.8277025938204418 By default, these operations apply to the assortment as though it were a list of numbers, regardless of its shape. However, by specifying the axis parameter you lot can apply an functioning along the specified axis of an array:
>>> b = np . arange ( 12 ) . reshape ( three , iv ) >>> b assortment([[ 0, 1, ii, 3], [ four, 5, 6, vii], [ 8, 9, 10, 11]]) >>> >>> b . sum ( axis = 0 ) # sum of each column array([12, 15, eighteen, 21]) >>> >>> b . min ( axis = ane ) # min of each row array([0, 4, 8]) >>> >>> b . cumsum ( axis = ane ) # cumulative sum along each row assortment([[ 0, 1, 3, vi], [ 4, ix, 15, 22], [ eight, 17, 27, 38]]) Universal Functions¶
NumPy provides familiar mathematical functions such as sin, cos, and exp. In NumPy, these are chosen "universal functions" ( ufunc ). Inside NumPy, these functions operate elementwise on an array, producing an array as output.
>>> B = np . arange ( 3 ) >>> B assortment([0, 1, 2]) >>> np . exp ( B ) array([1. , 2.71828183, seven.3890561 ]) >>> np . sqrt ( B ) array([0. , one. , i.41421356]) >>> C = np . array ([ 2. , - 1. , 4. ]) >>> np . add together ( B , C ) array([two., 0., vi.]) See likewise
all , whatever , apply_along_axis , argmax , argmin , argsort , boilerplate , bincount , ceil , clip , conj , corrcoef , cov , cross , cumprod , cumsum , diff , dot , flooring , inner , capsize , lexsort , max , maximum , mean , median , min , minimum , nonzero , outer , prod , re , round , sort , std , sum , trace , transpose , var , vdot , vectorize , where
Indexing, Slicing and Iterating¶
One-dimensional arrays can be indexed, sliced and iterated over, much similar lists and other Python sequences.
>>> a = np . arange ( ten ) ** 3 >>> a array([ 0, 1, eight, 27, 64, 125, 216, 343, 512, 729]) >>> a [ ii ] viii >>> a [ two : 5 ] array([ 8, 27, 64]) >>> # equivalent to a[0:half dozen:2] = thou; >>> # from start to position 6, exclusive, fix every 2nd element to 1000 >>> a [: half-dozen : 2 ] = 1000 >>> a array([1000, 1, thou, 27, 1000, 125, 216, 343, 512, 729]) >>> a [:: - 1 ] # reversed a array([ 729, 512, 343, 216, 125, g, 27, g, ane, m]) >>> for i in a : ... print ( i ** ( ane / 3. )) ... 9.999999999999998 i.0 9.999999999999998 three.0 9.999999999999998 4.999999999999999 5.999999999999999 6.999999999999999 7.999999999999999 8.999999999999998 Multidimensional arrays tin have ane index per axis. These indices are given in a tuple separated by commas:
>>> def f ( 10 , y ): ... render 10 * ten + y ... >>> b = np . fromfunction ( f , ( five , iv ), dtype = int ) >>> b array([[ 0, i, 2, 3], [ten, eleven, 12, 13], [20, 21, 22, 23], [30, 31, 32, 33], [twoscore, 41, 42, 43]]) >>> b [ 2 , 3 ] 23 >>> b [ 0 : 5 , 1 ] # each row in the 2d column of b assortment([ 1, 11, 21, 31, 41]) >>> b [:, ane ] # equivalent to the previous example assortment([ 1, 11, 21, 31, 41]) >>> b [ 1 : three , :] # each column in the second and third row of b assortment([[ten, xi, 12, xiii], [twenty, 21, 22, 23]]) When fewer indices are provided than the number of axes, the missing indices are considered complete slices :
>>> b [ - 1 ] # the last row. Equivalent to b[-1, :] array([40, 41, 42, 43]) The expression within brackets in b[i] is treated every bit an i followed by equally many instances of : equally needed to represent the remaining axes. NumPy also allows yous to write this using dots equally b[i, ...] .
The dots ( ... ) represent as many colons as needed to produce a complete indexing tuple. For example, if x is an array with v axes, so
-
ten[1, 2, ...]is equivalent tox[i, 2, :, :, :], -
10[..., 3]tox[:, :, :, :, 3]and -
ten[4, ..., five, :]tox[4, :, :, 5, :].
>>> c = np . array ([[[ 0 , one , two ], # a 3D array (2 stacked 2D arrays) ... [ x , 12 , thirteen ]], ... [[ 100 , 101 , 102 ], ... [ 110 , 112 , 113 ]]]) >>> c . shape (2, 2, 3) >>> c [ one , ... ] # aforementioned as c[1, :, :] or c[1] assortment([[100, 101, 102], [110, 112, 113]]) >>> c [ ... , 2 ] # same equally c[:, :, 2] array([[ 2, 13], [102, 113]]) Iterating over multidimensional arrays is done with respect to the kickoff centrality:
>>> for row in b : ... impress ( row ) ... [0 1 2 iii] [10 11 12 13] [20 21 22 23] [30 31 32 33] [40 41 42 43] However, if i wants to perform an performance on each chemical element in the array, one can use the apartment attribute which is an iterator over all the elements of the array:
>>> for element in b . apartment : ... impress ( element ) ... 0 1 2 3 10 11 12 thirteen xx 21 22 23 xxx 31 32 33 twoscore 41 42 43 Shape Manipulation¶
Changing the shape of an array¶
An assortment has a shape given by the number of elements along each axis:
>>> a = np . floor ( ten * rg . random (( 3 , 4 ))) >>> a array([[iii., 7., 3., 4.], [i., 4., ii., ii.], [seven., 2., iv., ix.]]) >>> a . shape (3, four) The shape of an array can be changed with various commands. Notation that the following three commands all return a modified assortment, merely do not change the original assortment:
>>> a . ravel () # returns the array, flattened array([3., 7., 3., 4., 1., iv., 2., 2., vii., 2., iv., 9.]) >>> a . reshape ( half-dozen , ii ) # returns the array with a modified shape array([[3., 7.], [three., 4.], [one., 4.], [2., 2.], [7., ii.], [four., nine.]]) >>> a . T # returns the array, transposed array([[3., i., vii.], [seven., four., ii.], [iii., 2., 4.], [4., ii., 9.]]) >>> a . T . shape (4, 3) >>> a . shape (iii, 4) The order of the elements in the array resulting from ravel is normally "C-way", that is, the rightmost index "changes the fastest", so the chemical element after a[0, 0] is a[0, 1] . If the array is reshaped to another shape, again the array is treated equally "C-manner". NumPy usually creates arrays stored in this gild, so ravel will normally not demand to copy its statement, but if the assortment was made by taking slices of some other assortment or created with unusual options, it may need to be copied. The functions ravel and reshape tin also be instructed, using an optional argument, to use FORTRAN-style arrays, in which the leftmost index changes the fastest.
The reshape function returns its argument with a modified shape, whereas the ndarray.resize method modifies the assortment itself:
>>> a array([[3., vii., 3., 4.], [1., 4., 2., two.], [7., 2., 4., ix.]]) >>> a . resize (( two , vi )) >>> a array([[3., 7., 3., 4., 1., four.], [two., ii., 7., ii., 4., 9.]]) If a dimension is given as -i in a reshaping operation, the other dimensions are automatically calculated:
>>> a . reshape ( 3 , - 1 ) array([[3., 7., 3., 4.], [1., 4., 2., 2.], [vii., 2., 4., 9.]]) Stacking together unlike arrays¶
Several arrays tin can be stacked together along different axes:
>>> a = np . floor ( 10 * rg . random (( 2 , ii ))) >>> a array([[9., 7.], [5., 2.]]) >>> b = np . floor ( 10 * rg . random (( ii , 2 ))) >>> b array([[1., 9.], [5., 1.]]) >>> np . vstack (( a , b )) assortment([[9., vii.], [5., 2.], [1., 9.], [5., one.]]) >>> np . hstack (( a , b )) array([[nine., 7., 1., nine.], [5., two., 5., one.]]) The function column_stack stacks 1D arrays every bit columns into a 2D array. Information technology is equivalent to hstack merely for 2D arrays:
>>> from numpy import newaxis >>> np . column_stack (( a , b )) # with 2D arrays array([[ix., 7., i., 9.], [5., two., v., 1.]]) >>> a = np . array ([ iv. , 2. ]) >>> b = np . array ([ 3. , eight. ]) >>> np . column_stack (( a , b )) # returns a 2D assortment array([[4., 3.], [2., 8.]]) >>> np . hstack (( a , b )) # the result is different array([4., 2., iii., 8.]) >>> a [:, newaxis ] # view `a` equally a second column vector array([[iv.], [2.]]) >>> np . column_stack (( a [:, newaxis ], b [:, newaxis ])) array([[4., 3.], [2., 8.]]) >>> np . hstack (( a [:, newaxis ], b [:, newaxis ])) # the result is the same array([[four., 3.], [two., 8.]]) On the other hand, the part row_stack is equivalent to vstack for any input arrays. In fact, row_stack is an allonym for vstack :
>>> np . column_stack is np . hstack Faux >>> np . row_stack is np . vstack True In general, for arrays with more than two dimensions, hstack stacks along their second axes, vstack stacks along their first axes, and concatenate allows for an optional arguments giving the number of the axis forth which the chain should happen.
Notation
In circuitous cases, r_ and c_ are useful for creating arrays by stacking numbers forth one axis. They permit the use of range literals : .
>>> np . r_ [ i : four , 0 , four ] array([1, 2, iii, 0, 4]) When used with arrays equally arguments, r_ and c_ are like to vstack and hstack in their default beliefs, but allow for an optional argument giving the number of the axis along which to concatenate.
Splitting i array into several smaller ones¶
Using hsplit , you can split an array along its horizontal centrality, either by specifying the number of equally shaped arrays to return, or by specifying the columns subsequently which the division should occur:
>>> a = np . floor ( ten * rg . random (( 2 , 12 ))) >>> a assortment([[6., 7., 6., ix., 0., 5., 4., 0., 6., eight., v., ii.], [8., 5., 5., 7., 1., 8., 6., 7., 1., 8., 1., 0.]]) >>> # Divide `a` into three >>> np . hsplit ( a , 3 ) [array([[6., seven., half dozen., 9.], [8., 5., 5., 7.]]), assortment([[0., 5., iv., 0.], [1., 8., six., 7.]]), array([[half dozen., viii., 5., 2.], [1., eight., 1., 0.]])] >>> # Split `a` afterwards the 3rd and the quaternary column >>> np . hsplit ( a , ( three , 4 )) [array([[6., 7., half-dozen.], [8., 5., five.]]), array([[9.], [7.]]), array([[0., 5., four., 0., 6., 8., five., 2.], [1., 8., 6., 7., 1., 8., 1., 0.]])] vsplit splits along the vertical axis, and array_split allows ane to specify along which axis to split.
Copies and Views¶
When operating and manipulating arrays, their data is sometimes copied into a new assortment and sometimes not. This is ofttimes a source of confusion for beginners. There are iii cases:
No Re-create at All¶
Simple assignments make no re-create of objects or their data.
>>> a = np . array ([[ 0 , 1 , 2 , 3 ], ... [ 4 , five , 6 , 7 ], ... [ 8 , 9 , 10 , 11 ]]) >>> b = a # no new object is created >>> b is a # a and b are two names for the same ndarray object Truthful Python passes mutable objects as references, then role calls brand no copy.
>>> def f ( x ): ... print ( id ( x )) ... >>> id ( a ) # id is a unique identifier of an object 148293216 # may vary >>> f ( a ) 148293216 # may vary View or Shallow Copy¶
Different assortment objects can share the aforementioned data. The view method creates a new array object that looks at the same data.
>>> c = a . view () >>> c is a Simulated >>> c . base is a # c is a view of the data owned by a True >>> c . flags . owndata Imitation >>> >>> c = c . reshape (( ii , six )) # a'southward shape doesn't change >>> a . shape (3, 4) >>> c [ 0 , iv ] = 1234 # a's information changes >>> a assortment([[ 0, 1, 2, iii], [1234, 5, six, 7], [ 8, 9, ten, 11]]) Slicing an array returns a view of it:
>>> s = a [:, i : 3 ] >>> due south [:] = 10 # s[:] is a view of s. Annotation the difference between southward = 10 and s[:] = 10 >>> a assortment([[ 0, 10, 10, 3], [1234, 10, ten, 7], [ 8, x, 10, 11]]) Deep Re-create¶
The copy method makes a complete re-create of the array and its information.
>>> d = a . re-create () # a new array object with new data is created >>> d is a False >>> d . base is a # d doesn't share anything with a False >>> d [ 0 , 0 ] = 9999 >>> a array([[ 0, 10, ten, 3], [1234, 10, 10, vii], [ 8, ten, ten, 11]]) Sometimes copy should be called after slicing if the original array is non required anymore. For example, suppose a is a huge intermediate upshot and the last consequence b only contains a small fraction of a , a deep re-create should be made when constructing b with slicing:
>>> a = np . arange ( int ( 1e8 )) >>> b = a [: 100 ] . re-create () >>> del a # the memory of ``a`` tin be released. If b = a[:100] is used instead, a is referenced past b and will persist in memory even if del a is executed.
Functions and Methods Overview¶
Here is a list of some useful NumPy functions and methods names ordered in categories. See Routines for the total list.
- Array Creation
-
arange,array,copy,empty,empty_like,middle,fromfile,fromfunction,identity,linspace,logspace,mgrid,ogrid,ones,ones_like,r_,zeros,zeros_like - Conversions
-
ndarray.astype,atleast_1d,atleast_2d,atleast_3d,mat - Manipulations
-
array_split,column_stack,concatenate,diagonal,dsplit,dstack,hsplit,hstack,ndarray.item,newaxis,ravel,repeat,reshape,resize,squeeze,swapaxes,take,transpose,vsplit,vstack - Questions
-
all,any,nonzero,where - Ordering
-
argmax,argmin,argsort,max,min,ptp,searchsorted,sort - Operations
-
choose,compress,cumprod,cumsum,inner,ndarray.fill,imag,prod,put,putmask,real,sum - Basic Statistics
-
cov,mean,std,var - Basic Linear Algebra
-
cross,dot,outer,linalg.svd,vdot
Less Bones¶
Broadcasting rules¶
Broadcasting allows universal functions to bargain in a meaningful way with inputs that exercise not accept exactly the same shape.
The kickoff dominion of broadcasting is that if all input arrays do not have the same number of dimensions, a "1" will exist repeatedly prepended to the shapes of the smaller arrays until all the arrays have the same number of dimensions.
The 2nd rule of broadcasting ensures that arrays with a size of 1 forth a particular dimension act as if they had the size of the assortment with the largest shape forth that dimension. The value of the array element is assumed to be the same along that dimension for the "broadcast" array.
Afterward application of the dissemination rules, the sizes of all arrays must match. More details tin can exist constitute in Dissemination.
Advanced indexing and index tricks¶
NumPy offers more than indexing facilities than regular Python sequences. In addition to indexing by integers and slices, as we saw before, arrays can exist indexed by arrays of integers and arrays of booleans.
Indexing with Arrays of Indices¶
>>> a = np . arange ( 12 ) ** 2 # the first 12 square numbers >>> i = np . assortment ([ 1 , 1 , 3 , 8 , 5 ]) # an array of indices >>> a [ i ] # the elements of `a` at the positions `i` array([ 1, 1, 9, 64, 25]) >>> >>> j = np . array ([[ 3 , 4 ], [ 9 , 7 ]]) # a bidimensional array of indices >>> a [ j ] # the same shape as `j` assortment([[ 9, sixteen], [81, 49]]) When the indexed array a is multidimensional, a single assortment of indices refers to the first dimension of a . The following example shows this beliefs by converting an paradigm of labels into a color image using a palette.
>>> palette = np . array ([[ 0 , 0 , 0 ], # blackness ... [ 255 , 0 , 0 ], # red ... [ 0 , 255 , 0 ], # light-green ... [ 0 , 0 , 255 ], # bluish ... [ 255 , 255 , 255 ]]) # white >>> paradigm = np . array ([[ 0 , 1 , ii , 0 ], # each value corresponds to a color in the palette ... [ 0 , iii , 4 , 0 ]]) >>> palette [ image ] # the (ii, 4, iii) color paradigm array([[[ 0, 0, 0], [255, 0, 0], [ 0, 255, 0], [ 0, 0, 0]], [[ 0, 0, 0], [ 0, 0, 255], [255, 255, 255], [ 0, 0, 0]]]) Nosotros can also give indexes for more than one dimension. The arrays of indices for each dimension must accept the aforementioned shape.
>>> a = np . arange ( 12 ) . reshape ( 3 , 4 ) >>> a assortment([[ 0, one, ii, iii], [ 4, 5, vi, seven], [ eight, nine, ten, xi]]) >>> i = np . array ([[ 0 , 1 ], # indices for the first dim of `a` ... [ 1 , 2 ]]) >>> j = np . array ([[ two , ane ], # indices for the second dim ... [ 3 , 3 ]]) >>> >>> a [ i , j ] # i and j must accept equal shape array([[ ii, 5], [ 7, 11]]) >>> >>> a [ i , ii ] array([[ 2, six], [ 6, 10]]) >>> >>> a [:, j ] assortment([[[ 2, 1], [ 3, three]], [[ vi, 5], [ 7, 7]], [[10, 9], [11, xi]]]) In Python, arr[i, j] is exactly the aforementioned as arr[(i, j)] —so we tin put i and j in a tuple and then do the indexing with that.
>>> fifty = ( i , j ) >>> # equivalent to a[i, j] >>> a [ l ] assortment([[ 2, 5], [ 7, 11]]) Notwithstanding, we can non practice this past putting i and j into an array, because this array will be interpreted as indexing the beginning dimension of a .
>>> s = np . array ([ i , j ]) >>> # not what we want >>> a [ s ] Traceback (most recent telephone call last): File "<stdin>", line one, in <module> IndexError: index 3 is out of bounds for axis 0 with size 3 >>> # same every bit `a[i, j]` >>> a [ tuple ( s )] array([[ 2, v], [ 7, 11]]) Some other common utilise of indexing with arrays is the search of the maximum value of fourth dimension-dependent series:
>>> fourth dimension = np . linspace ( 20 , 145 , 5 ) # fourth dimension scale >>> data = np . sin ( np . arange ( 20 )) . reshape ( 5 , 4 ) # 4 fourth dimension-dependent series >>> time assortment([ twenty. , 51.25, 82.5 , 113.75, 145. ]) >>> data array([[ 0. , 0.84147098, 0.90929743, 0.14112001], [-0.7568025 , -0.95892427, -0.2794155 , 0.6569866 ], [ 0.98935825, 0.41211849, -0.54402111, -0.99999021], [-0.53657292, 0.42016704, 0.99060736, 0.65028784], [-0.28790332, -0.96139749, -0.75098725, 0.14987721]]) >>> # index of the maxima for each series >>> ind = data . argmax ( axis = 0 ) >>> ind array([2, 0, 3, i]) >>> # times corresponding to the maxima >>> time_max = time [ ind ] >>> >>> data_max = data [ ind , range ( data . shape [ one ])] # => data[ind[0], 0], data[ind[1], ane]... >>> time_max array([ 82.5 , xx. , 113.75, 51.25]) >>> data_max array([0.98935825, 0.84147098, 0.99060736, 0.6569866 ]) >>> np . all ( data_max == data . max ( centrality = 0 )) Truthful You can also utilise indexing with arrays every bit a target to assign to:
>>> a = np . arange ( 5 ) >>> a array([0, 1, ii, iii, 4]) >>> a [[ 1 , 3 , 4 ]] = 0 >>> a assortment([0, 0, ii, 0, 0]) Nonetheless, when the list of indices contains repetitions, the assignment is done several times, leaving behind the terminal value:
>>> a = np . arange ( v ) >>> a [[ 0 , 0 , 2 ]] = [ one , 2 , 3 ] >>> a assortment([ii, 1, 3, three, 4]) This is reasonable enough, but spotter out if yous want to use Python'southward += construct, every bit information technology may non do what you expect:
>>> a = np . arange ( 5 ) >>> a [[ 0 , 0 , two ]] += 1 >>> a array([1, 1, 3, 3, iv]) Even though 0 occurs twice in the list of indices, the 0th element is only incremented once. This is because Python requires a += i to be equivalent to a = a + 1 .
Indexing with Boolean Arrays¶
When nosotros alphabetize arrays with arrays of (integer) indices we are providing the list of indices to pick. With boolean indices the arroyo is different; nosotros explicitly choose which items in the assortment nosotros want and which ones we don't.
The most natural way one can call up of for boolean indexing is to use boolean arrays that accept the same shape as the original array:
>>> a = np . arange ( 12 ) . reshape ( 3 , iv ) >>> b = a > 4 >>> b # `b` is a boolean with `a`'s shape array([[Faux, False, False, False], [False, True, True, Truthful], [ True, True, True, True]]) >>> a [ b ] # 1d array with the selected elements array([ 5, 6, vii, 8, 9, 10, eleven]) This property can be very useful in assignments:
>>> a [ b ] = 0 # All elements of `a` higher than 4 become 0 >>> a array([[0, i, 2, 3], [4, 0, 0, 0], [0, 0, 0, 0]]) You can look at the following example to run into how to apply boolean indexing to generate an image of the Mandelbrot set up:
>>> import numpy equally np >>> import matplotlib.pyplot equally plt >>> def mandelbrot ( h , w , maxit = 20 , r = 2 ): ... """Returns an prototype of the Mandelbrot fractal of size (h,w).""" ... x = np . linspace ( - ii.5 , 1.v , 4 * h + 1 ) ... y = np . linspace ( - one.5 , 1.5 , iii * w + 1 ) ... A , B = np . meshgrid ( x , y ) ... C = A + B * i j ... z = np . zeros_like ( C ) ... divtime = maxit + np . zeros ( z . shape , dtype = int ) ... ... for i in range ( maxit ): ... z = z ** ii + C ... diverge = abs ( z ) > r # who is diverging ... div_now = diverge & ( divtime == maxit ) # who is diverging now ... divtime [ div_now ] = i # note when ... z [ diverge ] = r # avoid diverging too much ... ... render divtime >>> plt . imshow ( mandelbrot ( 400 , 400 )) 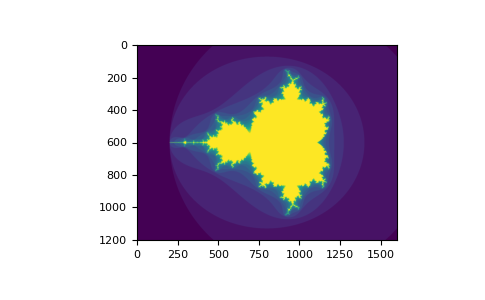
The second way of indexing with booleans is more than similar to integer indexing; for each dimension of the array we give a 1D boolean array selecting the slices we desire:
>>> a = np . arange ( 12 ) . reshape ( 3 , 4 ) >>> b1 = np . array ([ Faux , Truthful , Truthful ]) # first dim selection >>> b2 = np . array ([ True , False , True , Simulated ]) # second dim selection >>> >>> a [ b1 , :] # selecting rows array([[ 4, v, six, 7], [ 8, ix, 10, 11]]) >>> >>> a [ b1 ] # same thing array([[ 4, five, 6, 7], [ 8, 9, ten, xi]]) >>> >>> a [:, b2 ] # selecting columns array([[ 0, 2], [ 4, 6], [ eight, ten]]) >>> >>> a [ b1 , b2 ] # a weird matter to do array([ 4, 10]) Note that the length of the 1D boolean array must coincide with the length of the dimension (or axis) you want to slice. In the previous example, b1 has length 3 (the number of rows in a ), and b2 (of length 4) is suitable to index the 2d axis (columns) of a .
The ix_() part¶
The ix_ function can be used to combine different vectors so as to obtain the upshot for each n-uplet. For example, if you want to compute all the a+b*c for all the triplets taken from each of the vectors a, b and c:
>>> a = np . assortment ([ two , 3 , 4 , 5 ]) >>> b = np . array ([ 8 , 5 , 4 ]) >>> c = np . array ([ five , 4 , half dozen , 8 , 3 ]) >>> ax , bx , cx = np . ix_ ( a , b , c ) >>> ax array([[[2]], [[three]], [[4]], [[5]]]) >>> bx array([[[8], [5], [4]]]) >>> cx assortment([[[v, 4, 6, viii, 3]]]) >>> ax . shape , bx . shape , cx . shape ((4, i, 1), (1, 3, 1), (1, 1, 5)) >>> result = ax + bx * cx >>> upshot array([[[42, 34, fifty, 66, 26], [27, 22, 32, 42, 17], [22, eighteen, 26, 34, xiv]], [[43, 35, 51, 67, 27], [28, 23, 33, 43, 18], [23, 19, 27, 35, 15]], [[44, 36, 52, 68, 28], [29, 24, 34, 44, 19], [24, xx, 28, 36, sixteen]], [[45, 37, 53, 69, 29], [thirty, 25, 35, 45, 20], [25, 21, 29, 37, 17]]]) >>> result [ three , 2 , 4 ] 17 >>> a [ 3 ] + b [ two ] * c [ 4 ] 17 You could as well implement the reduce as follows:
>>> def ufunc_reduce ( ufct , * vectors ): ... vs = np . ix_ ( * vectors ) ... r = ufct . identity ... for v in vs : ... r = ufct ( r , five ) ... return r and then use it as:
>>> ufunc_reduce ( np . add together , a , b , c ) array([[[15, xiv, 16, 18, 13], [12, 11, 13, 15, ten], [11, 10, 12, 14, 9]], [[sixteen, 15, 17, 19, fourteen], [13, 12, fourteen, xvi, 11], [12, 11, 13, xv, 10]], [[17, 16, xviii, twenty, 15], [14, thirteen, 15, 17, 12], [13, 12, fourteen, 16, eleven]], [[18, 17, 19, 21, xvi], [15, fourteen, xvi, 18, 13], [14, thirteen, fifteen, 17, 12]]]) The advantage of this version of reduce compared to the normal ufunc.reduce is that it makes use of the broadcasting rules in club to avert creating an argument assortment the size of the output times the number of vectors.
Indexing with strings¶
See Structured arrays.
Tricks and Tips¶
Here we give a list of short and useful tips.
"Automatic" Reshaping¶
To alter the dimensions of an array, you lot can omit one of the sizes which will then be deduced automatically:
>>> a = np . arange ( xxx ) >>> b = a . reshape (( ii , - ane , 3 )) # -1 means "whatever is needed" >>> b . shape (2, 5, iii) >>> b assortment([[[ 0, one, 2], [ 3, four, 5], [ 6, 7, 8], [ 9, x, eleven], [12, 13, xiv]], [[xv, xvi, 17], [xviii, 19, 20], [21, 22, 23], [24, 25, 26], [27, 28, 29]]]) Vector Stacking¶
How do we construct a 2nd assortment from a list of equally-sized row vectors? In MATLAB this is quite easy: if ten and y are two vectors of the same length y'all just need do m=[x;y] . In NumPy this works via the functions column_stack , dstack , hstack and vstack , depending on the dimension in which the stacking is to be done. For example:
>>> x = np . arange ( 0 , ten , 2 ) >>> y = np . arange ( 5 ) >>> m = np . vstack ([ x , y ]) >>> m assortment([[0, 2, 4, 6, 8], [0, 1, two, three, 4]]) >>> xy = np . hstack ([ x , y ]) >>> xy assortment([0, ii, 4, six, 8, 0, 1, 2, 3, four]) The logic behind those functions in more than 2 dimensions tin be strange.
Histograms¶
The NumPy histogram function applied to an array returns a pair of vectors: the histogram of the array and a vector of the bin edges. Beware: matplotlib also has a function to build histograms (called hist , equally in Matlab) that differs from the i in NumPy. The main divergence is that pylab.hist plots the histogram automatically, while numpy.histogram only generates the data.
>>> import numpy equally np >>> rg = np . random . default_rng ( 1 ) >>> import matplotlib.pyplot as plt >>> # Build a vector of 10000 normal deviates with variance 0.5^2 and mean 2 >>> mu , sigma = 2 , 0.5 >>> five = rg . normal ( mu , sigma , 10000 ) >>> # Plot a normalized histogram with fifty bins >>> plt . hist ( v , bins = 50 , density = True ) # matplotlib version (plot) >>> # Compute the histogram with numpy and and then plot information technology >>> ( due north , bins ) = np . histogram ( v , bins = l , density = True ) # NumPy version (no plot) >>> plt . plot ( .5 * ( bins [ 1 :] + bins [: - 1 ]), due north ) 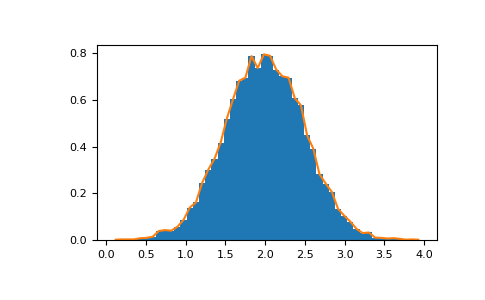
With Matplotlib >=iii.4 yous tin can also use plt.stairs(due north, bins) .
Further reading¶
-
The Python tutorial
-
NumPy Reference
-
SciPy Tutorial
-
SciPy Lecture Notes
-
A matlab, R, IDL, NumPy/SciPy dictionary
-
tutorial-svd
Source: https://numpy.org/doc/stable/user/quickstart.html
0 Response to "We Do It Again and Get a 5 and the Array 2 1 0 0 0 0 0 0"
Post a Comment